



次へ: Optically-Thin Thermal Free-Free Emission
上へ: Data Analysis
戻る: Curves of Flux, Circular
目次
Optically-Thin Non-Thermal Gyrosynchrotron Emission
Note: The procedures described in this subsection are under testing.
Comments are welcome for improvement.
Based on approximation models, the relation between
the physical variables of emitting region and the emission can be
derived. The electron distribution function is assumed to be
the power law.
where 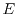 is electron energy (keV),
is electron energy (keV), 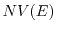 is number of electrons (particles)
that has larger energy than
is number of electrons (particles)
that has larger energy than 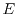 . This distribution is described with parameters
. This distribution is described with parameters
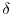 ,
, 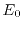 , and
, and 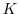 . But it is usual to use
. But it is usual to use
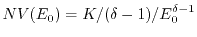 instead of
instead of 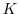 . And we fix
. And we fix
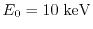 after Dulk (1985).
after Dulk (1985).
(a) From Physical Variables to Emission
Inputs; power-law index 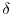 , magnetic field strength (G), angle between
magnetic field and line of sight (degree), and
, magnetic field strength (G), angle between
magnetic field and line of sight (degree), and 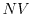 -- total number (particles) of non-thermal electron (of
-- total number (particles) of non-thermal electron (of
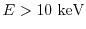 ):
Outputs; flux density (SFU), circular polarization degree:
):
Outputs; flux density (SFU), circular polarization degree:
By Dulk's (1985) method:
IDL> dulk_gysy,delta,bb,theta,nv,freq,fi,rc 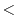 CR
CR
If the size of emitting source (by solid angle in unit of sterad) is given
additionally, optical depth is also obtained
IDL> dulk_gysy,delta,bb,theta,nv,freq,fi,rc,omega,tau 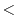 CR
CR
By Ramaty's (1969) method:
IDL> ramaty_gysy,delta,bb,theta,nv,freq,fi,rc  CR
CR
IDL> ramaty_gysy,delta,bb,theta,nv,freq,fi,rc,omega,tau  CR
CR
(b) From Emission to Physical Variables
Based on Dulk's (1985) model we may derive the physical variables from emission.
After deriving 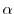 (see 4.5.9),
power law index of non-thermal electron distribution function is
(see 4.5.9),
power law index of non-thermal electron distribution function is
IDL> norh_alpha,indexa,fi17,indexz,fi34
,indexal,alpha,mvda 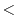 CR
CR
IDL> norh_alpha2delta,alpha,delta 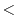 CR
CR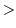
If V-component (R L) of 17 GHz is given adding to this,
physical variables can be derived to some extent. For this,
we have to assume one of three variables to be obtained --
magnetic field strength (G), angle between
magnetic field and line of sight (degree), and total number of non-thermal
electron of
L) of 17 GHz is given adding to this,
physical variables can be derived to some extent. For this,
we have to assume one of three variables to be obtained --
magnetic field strength (G), angle between
magnetic field and line of sight (degree), and total number of non-thermal
electron of
 (particles).
(particles).
IDL> norh_gysy_inv,fi17,fi34,delta,fv17,thetain,bb,nv,/assumetheta
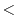 CR
CR
IDL> norh_gysy_inv,fi17,fi34,delta,fv17,bbin,nv,theta,/assumebb
 CR
CR
IDL> norh_gysy_inv,fi17,fi34,delta,fv17,nvin,theta,bb,/assumenv
 CR
CR
Adding to this, if the size of emission source is given
(as solid angle. Unit is sterad), optical thickness is derived
IDL> norh_gysy_inv,fi17,fi34,delta,fv17,thetain,bb,nv,/assumetheta
,omega,tau  CR
CR
IDL> norh_gysy_inv,fi17,fi34,delta,fv17,bbin,nv,theta,/assumebb
,omega,tau  CR
CR
IDL> norh_gysy_inv,fi17,fi34,delta,fv17,nvin,theta,bb,/assumenv
,omega,tau  CR
CR
Note: In case of images, make the size of beams same between two images
(see section 4.5.8).




次へ: Optically-Thin Thermal Free-Free Emission
上へ: Data Analysis
戻る: Curves of Flux, Circular
目次
service@solar.nro.nao.ac.jp