Interpretation of Data

図 5: Chart for interpretation of emission mechanism from the spectrum distribution

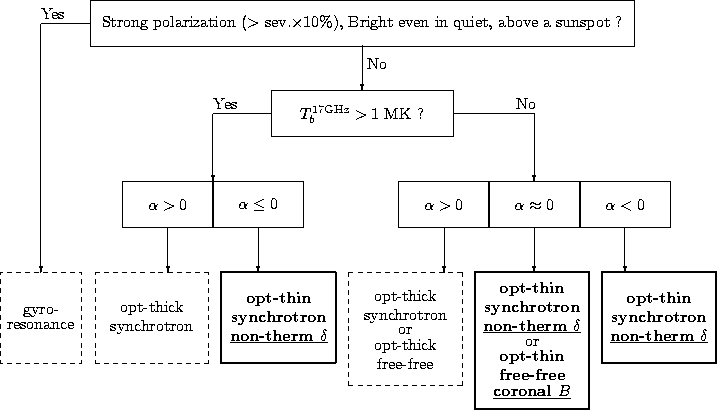
The interpretation is done by using the chart in Figure 5. Physical information can be obtained when the emission is by "optically-thin gyrosynchrotron" or by "optically-thin free-free". We can derive the variable using the Dulk's (1985) models.

In case "optically-thin gyrosynchrotron" emission, we obtain power-law index of the non-thermal electrons. Here we assume the distribution function of electrons to be

$${{d NV(E)} \over {d E}} = K \left({{E}\over{E_{0}}}\right)^{-\delta}.$$

where $E$ is electron energy (keV), $NV(E)$ is number of electrons (particles) that has larger energy than $E$. This distribution is described with parameters $\delta$, $E_{0}$, and $K$. But it is usual to use $NV(E_0)=K/(\delta -1)/E_0^{\delta-1}$ instead of $K$. And we fix $E_{0} = 10\ {\rm keV}$ after Dulk (1985). If we find the emission to be "optically-thin gyrosynchrotron", we will obtain $\delta$ from $\alpha$ by

$$\delta=-1.1 (\alpha - 1.2).$$

In case "optically-thin free-free" emission, we obtain line-of-sight component of coronal magnetic field. From the circular polarization degree $r_{c}$,

$$B \approx 30 {\rm G} \left({r_{c}\over 1\%}\right).$$

For example, figure 4 can be interpreted as follows: First, the strong polarized source at $(x,y)=(180,-520)$ is by gyroresonance. It may be confirmed by comparing the image with optical magnetogram to see if there is a sunspot. Next, the area inside the contour line of $T_{b}^{\rm 17GHz}=1{\rm MK}$ is emitting by optically-thin gyrosynchrotron. Non-thermal power-law index $\delta$ is obtained from $\alpha$ immediately and we see that the emission from two-sides of the loop structure is 'softer' than that of the top. Next is for the area where $T_{b}^{\rm 17GHz}<1{\rm MK}$. Around $(x,y)=(270,-500)$, it is hard to judge if it is 'optically-thin gyrosynchrotron' or "optically-thin free-free" because $\alpha \approx 0$. If it is bright in soft X-ray it may be free-free emission. In this case, line-of-sight component of coronal magnetic field is obtained. Since the other area has $\alpha>0$, it is optically thick and no information can be obtained.